~3000BC A papyrus, that was bought in a Luxor antique shop by Edwin Smith in 1882, was prepared representing 48 surgical observations of head wounds. The observations were stated in symptom-diagnosis-treatment-prognosis combinations as: IF a patient has this symptom, THEN he has this injury with this prognosis if this treatment is applied. This was the first known expert system. 13th C Ramón Lull invented the Zairja, the first device that systematically tried to generate ideas by mechanical means. 1651 Leviathan, written by Thomas Hobbes (1588–1679), was published. In it he proposes that humans collectively, by virtue of their organization and use of their machines, would create a new intelligence. George B. Dyson refers to Hobbes as the patriarch of artificial intelligence in his book, "Darwin Among the Machines: The Evolution of Global Intelligence," p7, 1997. 17th C Leibnitz and Pascal invented mechanical computing devices. Pascal was 19 years old in 1642 when he invented an eight-digit calculator, the Pascaline. In 1694, Gottfried Liebnitz invented the Liebnitz Computer, which multiplied by repetitive addition, an algorithm still in use today. Leibnitz also conceived of a 'reasoning calculator' for interpreting and evaluating concepts, but realized the problem was immense because of the great interconnectedness of concepts. 1726 Jonathan Swift anticipated an automatic book writer in Gulliver's Travels. 1805 Joseph-Marie Jacquard invented the first truly programmable device to drive looms with instructions provided by punched cards. 1832 Charles Babbage designed the 'analytical engine,' a mechanical programmable computer. He had earlier designed a more limited Difference Engine in 1822, which he never finished building. 1847 George Boole developed a mathematical symbolic logic (later called Boolean algebra) for reasoning about categories (i.e., sets) of objects, which is also applicable to manipulating and simplifying logical propositions. 1879 Gottlob Frege went beyond Boole in his treatment of logic with his invention of predicate logic, making it possible to prove general theorems from rules. However, the meaning of the words being manipulated by this logic is still only what the user intended, and therefore not conveyed by his representation of the logic. ~1890 Hand-driven mechanical calculators became available. 1890 Herman Hollerith patented a tabulating machine to process census data fed in on punched cards. His company, the Tabulating Machine Company, eventually merged into what was to become IBM. Late 1800s Leonardo Torres y Quevedo invented a relay-activated automaton that played end games in chess. 1898 Behaviorism was expounded by psychologist Edward Lee Thorndike in "Animal Intelligence." The basic idea is that all actions, thoughts, or desires are reflexes triggered by a higher form of stimulus, with humans just reacting to a higher form of stimulus. Mind, according to behaviorism, becomes a trivial concept, a passive associative mechanism. 1921 Karel Capek, a Czech writer, invented the term robot to describe intelligent machines that revolted against their human masters and destroyed them. 1928 John von Neumann introduced the minimax theorem, which is still used as a basis for game-playing programs. 1931 Vannevar Bush's mechanical differential analyzer (a mechanical analog computer) was able to solve differential equations. 1931 Kurt Godel demonstrated that math theorems we know to be true can be unprovable. This means that humans can recognize the true meaning of some sentences but the truth of them can't be derived by any logical system. 1937 Alan Turing conceived of a universal Turing machine that could mimic the operation of any other computing machine. However, as did Godel, he also recognized that there exists certain kinds of calculations that no machine could perform. Even recognizing this limit on computers, Turing still did not doubt that computers could be made to think. 1937 Alan Turing and Alonzo Church independently arrived at the same thesis, the Church-Turing thesis, that all problems that a human can solve can be reduced to a set of algorithms. ~1938 Claude Shannon showed that calculations could be performed much faster using electromagnetic relays than they could be performed with mechanical calculators. He applied Boolean algebra. Electromechanical relays were used in the world's first operational computer, Robinson, in 1940. Robinson was used by the English to decode messages from Enigma, the Germans' enciphering machine. 1943 Vacuum tubes replaced electromechanical relays in calculators. These were used in 1943 in Colossus, a faster successor to Robinson, to decipher increasingly complex German codes. 1943 Walter Pitts and Warren McCullock showed how artificial neural networks could compute, relying on the use of feedback loops. 1945 John von Neumann designed the basic computer architecture still used today, in which the memory stores instructions as well as data, and instructions are executed serially. He described this in a 1945 paper. 1945 ENIAC (Electronic Numerical Integrator and Calculator), which was to run 1,000 times faster than the relay-operated computers, was ready to run in late 1945. It was the first general purpose, programmable computer. John W. Mauchley and John Presper Eckert were its inventors. 1945—1956 Symbolic artificial intelligence emerged as a specific intellectual field. Key developments included Norbert Wiener's development of the field of cybernetics, in which he invented a mathematical theory of feedback in biological and engineered systems. This work helped clarify the concept that intelligence is the process of receiving and processing information to achieve goals. 1947 The transistor was invented by William Shockley, Walter Brattain, and John Bardeen. 1948 Nobert Wiener published Cybernetics, a landmark book on information theory. "Cybernetics" means "the science of control and communication in the animal and the machine." 1949 Donald O. Hebbs suggested a way in which artificial neural networks might learn. 1950 Turing proposed his test, the Turing test, to recognize machine intelligence. 1951 EDVAC, the first von Neumann computer, was built. 1951 Marvin Minsky and Dean Edmonds build the first artificial neural network that simulated a rat finding its way through a maze. 7 June 1954 Turing suicided in mysterious circumstances by eating a cyanide-laced apple following a conviction for homosexuality in 1953. 1950s It became clear that computers could manipulate symbols representing concepts as well as numerical data. 1955 - 1956 Logic Theorist, the first AI program, was written by Allen Newell, Herbert Simon, and J.C. Shaw. It proved theorems using a combination of searching, goal-oriented behavior, and application of rules. It used a list-processing technique in a new computer language, IPL (Information Processing Language) that they developed to write Logical Theorist. IPL provided pointers between related pieces of information to mimic associative memory; and catered to creating, changing, and destroying interacting symbolic structures on the fly. ~1956 IBM released the 701 general purpose electronic computer, the first such machine on the market. It was designed by Nathaniel Rochester. 1956 A two-month summer conference on thinking machines was held at Dartmouth University. The attendees included John McCarthy, Marvin Minsky, Claude Shannon, Nathaniel Rochester, Ray Solomonoff, Oliver Selfridge, Trenchard More, Arthur Samuel, Herbert Simon, and Allen Newell. It did not result in a consensus view of AI. "Every aspect of learning or any other feature of intelligence can in principle be so precisely described that a machine can be made to simulate it." according to a statement of the Dartmouth conference participants, that expresses the physical symbol hypothesis. 1956 John McCarthy names the new discipline, "Artificial Intelligence." 1956 George Miller published "The Magic Number Seven" on the limits of short-term memory. 1956 - 1963 Two main themes emerge in AI: · improved search methods in trial-and-error problems · making computers learn by themselves (e.g., to play checkers better than the program's author) 1957 Newell and Simon ran the General Problem Solver incorporating "means-ends analysis." Means-ends analysis seeks to reduce the difference between the predicted outcome and desired outcome by changing controlling factors. GPS and later AI programs were really quite limited in their problem solving ability as the programmer had to feed information to it in a highly stylized way. They also had to work hard to define each new problem, and the program made only a small contribution to the solution. Also, these programs contributed nothing to providing motivation for solving a problem, still an open issue today. Edward Feigenbaum's EPAM (Elementary Perceiver and Memorizer), provided a model of how people memorize nonsense syllables. Herbert Gelernter wrote the Geometry Theorem Prover which used information to prune a search with a billion alternatives (for a 3-step proof of a geometry theorem) to only 25 alternatives. He was the first to demonstrate "model referencing." Arthur Samuel wrote a checkers-playing program that soon learned how to beat him. 1957 Noam Chomsky, a linguist at MIT, postulated that language could be analyzed without reference to its content or meaning. In other words, syntax was independent of semantics. This concept was enticing to AI people as it would mean knowledge could be represented and analyzed without knowing anything about what was being said. Experience has shown that this concept doesn't apply well to human languages. 1958 John McCarthy and Marvin Minsky founded the Artificial Intelligence Laboratory at the Massachusetts Institute of Technology. 1958 John McCarthy developed the LISP program at MIT for AI work. It soon supplanted the earlier AI language, IPL, and retained its popularity against a later language, COMIT, developed in 1962. Early 1960s AI researchers concentrated on means of representing related knowledge in computers, a necessary precursor to developing the ability of computers to learn. 1961 Mortimer Taube, an engineer, authored the first anti-AI book, "Computers and Common Sense: The Myth of Thinking Machines." It did not receive much attention. 1962 The world's first industrial robots were marketed by a U.S. company. 1963 Tom Evans, under Marvin Minsky's supervision, created the program, ANALOGY. It was designed to solve problems that involved associating geometric patterns that occurred in a past case with the pattern in a current case. ANALOGY could solve shape problems of the kind, figure C is to which of several alternative figures as figure A is to figure B. 1963 The Stanford University founded the Artificial Intelligence Laboratory under John McCarthy. 1965 Brothers, Herbert L. Dreyfus, a philosopher, and Stuart E. Dreyfus, a mathematician, wrote a strongly anti-AI paper, "Alchemy and AI," which was published reluctantly by the RAND Corporation for whom Herbert was consulting. 1965 Herbert Simon predicted that machines will be capable of doing any work a man can do by 1985. 1965 The Robotics Institute was started at Carnegie Mellon University under Raj Reddy. 1965 to ~1975 Edward Feigenbaum and Robert K. Lindsay at Stanford built DENDRAL, the first expert system. Its expertise was in mapping the structure of complex organic chemicals from data gathered by mass spectrometers. After DENDRAL's rules grew to a certain size, its tangled set of statements became difficult to maintain and expand. Middle and late 1960s Marvin Minsky and Seymour Papert directed the Blocks Microworld Project at MIT AI Laboratory. This project improved computer vision, robotics, and even natural language processing enough for computers to view and manipulate a simple world of blocks of different colors, shapes, and sizes. Similar experiments proceeded at Stanford under John McCarthy and at Edinburgh University. 1966 National Research Council ended all support for automatic translation research, a field closely related to AI. 1968 The tradition of mad computers is continued with the release of the film, 2001: A Space Odyssey, directed by Stanley Kubrick, from Arthur C. Clarkes' book. The computer's name, HAL, is a reminder of the giant computer company, IBM. (Form a word from the letters that come after H, A, and L in the alphabet.) 1968 & 1969 Terry Winograd, a doctoral student under Seymour Papert, wrote SHRDLU (a word used in MAD magazine for mythical monsters and other oddities). SHRDLU created a simulated block world and robotic arm on a computer about which a user could ask questions and give commands in ordinary English. It has gradually been realized that the techniques employed in SHRDLU would not work beyond artificially defined toy worlds or restricted areas of expertise because, to do so, the computer would have to know vast amounts of knowledge that humans regard as common knowledge or common sense. 1969 - 1974 Roger Schank developed his "conceptual dependency" theory which enabled computers to make more plausible inferences about the meaning of the "semantic primitives" in sentences, when words took on secondary meanings. For example, the meanings of sentences such as "He gave her a present," and "Bill gave Joe a glancing blow" could be distinguished. However, the theory was inadequate for dealing with the complexities of meaning possible in linked sentences narrating a sequence of events, when some of the events can only be inferred from what is said. Typically, humans can readily infer the unstated events in a specific sequence. 1969 A mobile robot called Shakey was assembled at Stanford, that could navigate a block world in eight rooms and follow instructions in a simplified form of English. 1969 Marvin Minsky and Seymour Papert published their book, Perceptrons—An Introduction to Computational Geometry. Until its publication work on artificial networks in the U.S. was flourishing, which this book brought to a near halt until the 1980s by disparaging some of this work. 1969 John McCarthy and Patrick J. Hayes reappraised how AI might usefully proceed. They discounted possible help from philosophy as "philosophers have not really come to agreement in 2500 years." They identified two basic problems to overcome . One is the "frame problem," that of managing all that is going on around the central actors, a task that creates a heavy computational burden. Next is the "qualification problem," meaning the need to deal with all the qualifiers that can arise to stop an expected rule from being followed exactly. For example, if the ignition key of a car is turned, usually the engine starts. However, there are many exceptions, such as when the car has no fuel, or the battery is discharged. 1970 William Wood at Bolte, Beranek & Newman in Boston conceived a parsing scheme called the Augmented Transition Network. By mixing syntax rules with semantic analysis, the scheme could discriminate between the meanings of sentences such as "The beach is sweltering" and "The boy is sweltering." 1970s Earlier machine learning efforts aimed at enabling computers to automatically optimize appropriate weights for variables they had been told were important to solving a problem. Now efforts were directed to automatically deriving those variables themselves—in other words, automatic concept formation. Douglas Lenat programmed Automated Mathematician (AM), a program to rediscover number theory by itself. It combined a set of rudimentary ideas, a sense of experimentation, and a sense of rightness of good discoveries to guide its activities, the latter two capabilities expressed in a number of rules (or heuristics). Despite some initial dramatic success, it quickly reached limits for discovering new number theory. Lenat realized that it was because the heuristics it had been given were limited, and he decided it needed to be able to create new and useful discovery heuristics for itself. Over five years he developed this new ability in a successor program, EURISKO. EURISKO kept track of the performance of the heuristics it used, and dropped the ones that performed poorly, and modified and improved the better performing ones. The program was successfully used to improve the design of 3D computer chips. It even taught itself how to play a space-war game, Traveller TCS, and became the national champion in 1982 and 1983 with a radical approach to the game. Early 1970s DARPA's Speech Understanding Research (SUR) program, for which Carnegie Mellon was the prime contractor was brought to an abrupt end. Although goals were met, the product, which has a limited grammar, was not considered practical. AI researchers turned from research into the control and expression of knowledge (such as was demonstrated in the Micro Worlds project) to the manipulation of large amounts of knowledge. This was done in recognition of the limitations of successful programs such as SHDLU and GPS to be extended to tackle the more complex problems of the real world in useful ways. The earlier work reflected overly simplistic approximations of the ways the human mind works, and better approximations were required. Manipulation of larger amounts of information was also enabled by the increasing power of computers. Early 1970s First practical demonstration of the use of fuzzy logic for process control. Abe Mamdani and his student, Seto Assilian, at Queen Mary College (now Queen Mary and Westfield) in London used fuzzy logic to control the operation of a small steam engine. 1971-1972 Alain Colmerauer and Phillipe Roussel wrote the computer language, PROLOG (for PROgrammation en LOGique). It was revised in 1974 to force logical statements (i.e., IF ... THEN) to be written only in the Horn clause format. This permitted it to solve problems that required showing something was NOT true to be concluded in a finite number of steps. PROLOG became the favored AI language outside the U.S. where LISP still held sway. 1972 on Edward Shortliffe, a Stanford doctoral student under Bruce Buchanan, and others wrote MYCIN, an expert system to diagnose infectious blood diseases and recommend antibiotics, with dosage adjusted for patient's body weight. They also created the first expert system shell, that contained the inference engine, which contained the logic of how rules were to be applied. MYCIN could also deal with probabilistic rules, which DENDRAL couldn't. MYCIN could outperform human clinicians in some trials. A difficulty that arose during the writing of these and subsequent expert systems has been the extraction of the knowledge from human experts into the rules, the so-called knowledge engineering. 1972 Herbert Dreyfus expanded his "Alchemy and AI" paper into an aggressively anti-AI book, "What Computers Can't Do." 1973 Sir James Lighthill, Cambridge University's Lucasian Chair of Applied Mathematics, advised the British government to cease most AI research in Britain. 1974 Funding for AI research at MIT, Carnegie Mellon, and Stanford from DARPA was cut drastically as a result of recent disappointing results. By mid-1970s Diverging specialties in AI field emerged. These included Edward Feigenbaum's work on expert systems; Roger Shank on language analysis; Marvin Minsky on knowledge representation; Douglas Lenat on automatic learning and nature of heuristics; David Marr on machine vision; and others developing PROLOG. 1974 Paul J. Werbos invented the back-propagation algorithm, that enabled multilayer neural networks, that had the ability to perform classification operations beyond simple Perceptrons. Back-propagation was independently rediscovered in the early 1980s by David Rumelhat and David Parker. 1975 Marvin Minsky published a paper, "A Framework for Representing Knowledge," which he started with "It seems to me that the ingredients of most theories in artificial intelligence and in psychology have been on the whole too minute, local, and unstructured to account ... for the effectiveness of commonsense thought." He proposed that people thought in terms of generic "frames" within which we look for expected features (he called them "terminals") with anticipated properties ("markers"). Frames may be grouped or linked together into systems. So, we would have idealized "house" frames with features including walls, windows, doors and a roof, which we would use to recognize real houses by frame matching. These and other frames, say, of shops, churches, and schools, would build a town system. ~1977 Roger Schank and others augmented the conceptual dependency theory with the use of scripts (short stories of typical sequences of events that don't leave out any events) and the use of knowledge of people's plans and goals to make sense of stories told by people and to answer questions about those stories that would require inferences to be made to answer them. This combination resulted in successful language analysis programs such as Janet Kolodner's CYRUS, that thought of itself as Cyrus Vance, learned about his life from newspaper accounts, and could even surmise that Vance's wife and the Israel prime minister Begin's wife met at a social occasion to which it would be likely spouses would be invited. This in fact happened. Late 1970s First commercial expert system was developed. It was XCON (for eXpert CONfigurer), developed by John McDermott at Carnegie Mellon. He developed it for Digital Equipment Company, which started using it in January 1980 to help configure computer systems, deciding between all the options available for their VAX system. It grew from containing about 300 rules in 1979 to more than 3,000 and could configure more than 10 different computer systems. End of 1970s Practical, commercial applications of AI were still rare. July 1979 World champion backgammon player, Luigi Villa of Italy, became the first human champion of a board game to be defeated by a computer program, which was written by Hans Berliner of Carnegie Mellon. The program evaluated its moves by evaluating a weighted set of criteria that measured the goodness of a move. It did not use the alternative process of searching amongst all possible future moves and countermoves, a method used in chess, as there are too many alternatives in backgammon. 1980s Fuzzy logic was introduced in a fuzzy predictive system used to operate the automated subway trains in Sendai, Japan. This system, designed by Hitachi, reduced energy consumption by 10% and lowered the margin of error in stopping the trains at specified positions to less than 10 centimeters. 1980 First meeting of the American Association for Artificial Intelligence held in Stanford, California. 1980 Commercial AI products were only returning a few million dollars in revenue. 1980 First industrial application of a fuzzy controller by Danish cement manufacturer, F.L. Smidth & Co. A/S to regulate the operation of a cement kiln, which is a complex process subject to random disturbances that made it difficult for an operator to control. 1982 David Marr's book, "Vision," was published posthumously, Marr died of leukemia in 1980. It provided a new view of how the human brain used shading, steropsis, texture, edges, color, and the frame concept to recognize things. While he put vision firmly on the map as a major AI problem, many of his ideas turned out to be wrong. 1982 John Hopfield showed how networks of simple neurons could be given the ability to calculate. Early to mid 1980s A succession of early expert systems were built and put in use by companies. These included: · a hydrostatic and rotary bacteria-killing cooker diagnosis program at Campbell's Soup based on Aldo Cimino's knowledge; · a lathe and grinder diagnosis analyzer at GM's Saginaw plant using Charlie Amble's skills at listening for problems based on sounds; · a mineral prospecting expert system called PROSPECTOR that found a molybdenum deposit; · a Bell system that analyzed problems in telephone networks, and recommended solutions; · FOLIO, an investment portfolio advisor; and · WILLARD, a forecaster of large thunderstorms. AI groups were formed in many large companies to develop expert systems. Venture capitalists started investing in AI startups, and noted academics joined some of these companies. 1986 sales of AI-based hardware and software were $425 million. Much of the new business were developing specialized hardware (e.g., LISP computers) and software (e.g., expert system shells sold by Teknowledge, Intellicorp, and Inference) to help build better and less expensive expert systems. Low quality, but effective computer vision systems were also commercially launched successfully. 1984 GE built an expert system based on electric locomotive diagnosis knowledge of one expert, David Smith, who was close to retirement. Called the Diesel Electric Locomotive Troubleshooting Aid, it could diagnose 80% of breakdowns, and provide repair instructions. Mid 1980s Resurgence of neural network technology, with the publication of key papers by the Parallel Distributed Processing Study Group. Demonstrations of neural networks in diverse applications such as artificial speech generation, learning to play backgammon, and driving a vehicle illustrated the versatility of the technology. A build-up of commercial interest in neural nets followed, with over 300 small companies, mostly startup founded by researchers, competing by 1989. The classic boom-bust cycle of expert systems was being repeated. 1985 MIT's Media Laboratory, dedicated to researching media-related applications using computer science (including artificial intelligence) and sociology, was founded under Jerome Weisner and Nicholas Negroponte. 1985 Speech systems now able to provide any of the following: a large vocabulary, continuous speech recognition, or speaker independence. 1987 Etienne Wenger published his book, "Artificial Intelligence and Tutoring Systems: Computational and Cognitive Approaches to the Communication of Knowledge," a milestone in the development of intelligent tutoring systems. ~1987 Rule-based expert systems start to show limits to their commercially viable size. XCON, the Digital Equipment Company expert system had reached about 10,000 rules, and was increasingly expensive to maintain. Reasons for these limits include: · Inflexibility of these expert systems in applying rules, and the tunnel vision implied in their limited knowledge, that can result in poor conclusions. Expert systems couldn't reverse their logical conclusions if later given contradictory facts. For example, an expert system would conclude that Bill Smith has ten toes because Bill Smith is a person and all people have ten toes. However, it couldn't then deal with the fact that Bill Smith lost three toes in an industrial accident. A human, using "non-monotonic" reasoning, has no problem concluding Bill Smith has only seven toes. · Rule-based expert systems couldn't draw conclusions from similar past cases. Such analogical reasoning is a common method used by humans. Extracting knowledge from experts who reason analogically and converting that knowledge into rules is problematic. · As new rules are added to expert systems, it becomes increasingly difficult to decide the order in which active rules ought to be acted upon. Unexpected effects may occur as new rules are added. This behavior is called opacity. · Expert systems don't know what they don't know, and might therefore provide wrong answers to questions with answers outside their knowledge. This behavior is called "brittleness." · Expert systems can't share their knowledge between them because they really don't have any sense of the words they manipulate, and the same words in different expert systems may not be used in the same ways. · Expert systems can't learn, that is, they can't establish correspondence and analogies between objects and classes of objects. It was gradually realized that expert systems are limited to "any problem that can be and frequently is solved by your in-house expert in a 10 to 30 minute phone call," as expressed by Morris W. Firebaugh at the University of Wisconsin. End of 1980s Expert systems were increasingly used in industry, and other AI techniques were being implemented jointly with conventional software, often unnoticed but with beneficial effect. 1990s Emphasis on ontology began. Ontology is the study of the kinds of things that exist. In AI, the programs and sentences deal with various kinds of objects, and AI researchers study what these kinds are and what their properties are. 1990s and 2000s AI applications of many, seemingly unrelated kinds are quietly being commercialized in greater and greater numbers. Not all these applications work as well as desired, but they are continually improving. These include: · Automatic scheduling software to automatically create better project schedules faster · Advanced learning software that works like human tutor in teaching one-on-one with each student · Continuous speech recognition programs that accurately turn speech into text · Software to manage information for individuals, finding just the documents immediately needed from amongst million of documents, and automatically summarizing documents · Face-recognition systems · Washing machines that automatically adjust to different conditions to wash clothes better · Automatic mortgage underwriting systems · Automatic investment decision makers · Software that improves the prediction of daily revenues and staffing requirements for a business · Credit fraud detection systems · Help desk support systems that help find the right answer to any customer's question faster · Shopping bots on the web · Data mining tools · E-mail filters · Automated advice systems that personalize their responses · And many, many more. Many commercializers of such products and services aren't identifying their use of artificial intelligence in their products and services. Probably they're not doing so because "artificial intelligence" isn't perceived to sell, while improved intelligent solutions to a customer's problem does. 1994 The World Wide Web emerges. 1997 Deep Blue, a highly parallel 32-node IBM RS/6000 SP supercomputer, beat Gary Kasparov, world champion of chess. Deep Blue did this by calculating hundreds of million of alternative plays for a number of moves ahead. May 17, 1999 An artificial intelligence system, Remote Agent, was given primary control of a spacecraft for the first time. For two days Remote Agent ran on the on-board computer of Deep Space 1, while 60 million miles from earth. The goal of such control systems is to provide less costly, more capable control, that is more independent from ground control. Currently the difficult job of spacecraft control is done by a team of spacecraft engineers. Sharing control with onboard AI systems will enable these people to control more spacecraft, and for more ambitious missions than possible before to be undertaken. |
Sharing ICT/InfoSec information for free in a simple, precise and hopefully enjoyable way!
Sunday, 20 November 2011
Chronology of Artificial Intelligence
Sets, Bags and Sequences
Elementary or "naive" set theory is used to define basic mathematical structures. A set is an arbitrary collection of elements, which may be real or imaginary, physical or abstract. In mathematics, sets are usually composed of abstract things like numbers and points, but one can also talk about sets of apples, oranges, people, or canaries. In computer science, sets are composed of bits, bytes, pointers, and blocks of storage. In many applications, the elements are never defined, but are left as abstractions that could be represented in many different ways in the human brain, on a piece of paper, or in computer storage.
Curly braces are used to enclose a set specification. For small, finite sets, the specification of a set can be an exhaustive list of all its elements:
{1, 97, 63, 12}.
{1, 97, 63, 12}.
This specifies a set consisting of the four integers 1, 97, 63, and 12. Since the order of listing the elements is immaterial, the following specification is equivalent to the one above:
{12, 63, 97, 1}.
If the set is very large, like the set of all mammals, a complete listing is impossible. It is hard enough to enumerate all the people in a single city, let alone all the cats, dogs, mice, deer, sheep, and kangaroos in the entire world. For such sets, the specification must state some rule or property that determines which elements are in the set:
{x | vertebrate(x) and warmBlooded(x) and hasHair(x) and lactiferous(x)}This specification may be read the set of all x such that x is vertebrate, x is warm blooded, x has hair, and x is lactiferous. A given set may be specified in more than one way. The following four specifications all determine the same set:{1, 2, 3}{x | x is an integer and 0<x<4}{x | x is a positive integer, x divides 6, and x 6}{x | x=1 or x=2 or x=3}
6}{x | x=1 or x=2 or x=3}A set specification that lists all elements explicitly is called a definition by extension. A specification that states a property that must be true of each element is called a definition by intension. Only finite sets can be defined by extension. Infinite sets must always be defined by intension or by some operations upon other infinite sets that were previously defined by intension.
In any theory using sets, there are two privileged sets: the empty set {}, which contains no elements at all, and the universal set U, which contains every element that is being considered. In mathematical discussions, for example, the universal set may be the set of all integers Z or the set of all real numbers R. In most discussions, the universal set is usually defined at the beginning of the presentation. Thereafter, other sets are built up from U: subsets of U, pairs of elements of U, sets of sets of elements from U, etc.
Of all the operators that deal with sets, the most basic is  , which states whether a particular element is in a set: the notation x
, which states whether a particular element is in a set: the notation x S means that x is an element of the set S; it may also be read x is a member of the set S or simply x is in S. All other operators on sets can be defined in terms of
S means that x is an element of the set S; it may also be read x is a member of the set S or simply x is in S. All other operators on sets can be defined in terms of  . Let A and B be any two sets. Following are the common operators of set theory; listed for each one is its name, standard symbol, informal English definition, and formal definition in terms of
. Let A and B be any two sets. Following are the common operators of set theory; listed for each one is its name, standard symbol, informal English definition, and formal definition in terms of  :
:
 , which states whether a particular element is in a set: the notation x
, which states whether a particular element is in a set: the notation x S means that x is an element of the set S; it may also be read x is a member of the set S or simply x is in S. All other operators on sets can be defined in terms of
S means that x is an element of the set S; it may also be read x is a member of the set S or simply x is in S. All other operators on sets can be defined in terms of  . Let A and B be any two sets. Following are the common operators of set theory; listed for each one is its name, standard symbol, informal English definition, and formal definition in terms of
. Let A and B be any two sets. Following are the common operators of set theory; listed for each one is its name, standard symbol, informal English definition, and formal definition in terms of  :
:- Union. A
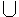 B is the set that contains all the elements in either A or B or both:
B is the set that contains all the elements in either A or B or both:A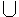 B = {x | x
B = {x | x A or x
A or x B}.
B}. - Intersection. A
 B is the set that contains all the elements that are in both A and B:
B is the set that contains all the elements that are in both A and B:A B = {x | x
B = {x | x A and x
A and x B}.
B}. - Complement. -A is the set that contains everything in the universal set that is not in A:
-A = {x | x U and not x
U and not x A}.
A}. - Difference. A-B is the set that contains all the elements that are in A but not in B:
A-B = {x | x A and not x
A and not x B}.
B}. - Subset. A
 B means that every element of A is also an element of B:
B means that every element of A is also an element of B:If x A, then x
A, then x B.
In particular, every set is a subset of itself: A
B.
In particular, every set is a subset of itself: A A.
A.
- Proper subset. A is a proper subset of B if A
 B and there is at least one element of B that is not in A:If x
B and there is at least one element of B that is not in A:If x A,then x
A,then x B and there exists some bwhere b
B and there exists some bwhere b B and not b
B and not b A.
A. - Superset. A is a superset of B if B is a subset of A.
- Empty set. The empty set has no elements: for every x, it is false that x
 {}. The empty set is a subset of every set, including itself: for every set A, {}
{}. The empty set is a subset of every set, including itself: for every set A, {} A.
A.
- Disjoint sets. Two sets A and B are said to be disjoint if they have no common elements; i.e., their intersection is the empty set: A
 B={}.
B={}.
The operators for union, intersection, and complement satisfy several standard identities. Some of the identities listed below are similar to the rules of ordinary arithmetic. Addition and multiplication, for example, obey the rules of commutativity and associativity, and the minus sign obeys the rule of double complementation. Idempotency, absorption, and De Morgan's laws, however, do not hold for ordinary arithmetic. Distributivity holds for multiplication over addition, but addition does not distribute over multiplication.
- Idempotency. A
 A is identical to A, and A
A is identical to A, and A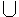 A is also identical to A.
A is also identical to A.
- Commutativity. A
 B is identical to B
B is identical to B A, and A
A, and A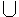 B is identical to B
B is identical to B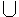 A.
A.
- Associativity. A
 (B
(B C) is identical to (A
C) is identical to (A B)
B) C, and A
C, and A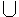 (B
(B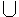 C) is identical to (A
C) is identical to (A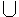 B)
B)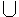 C.
C.
- Distributivity. A
 (B
(B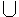 C) is identical to (A
C) is identical to (A B)
B)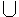 (A
(A C), and A
C), and A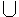 (B
(B C) is identical to (A
C) is identical to (A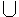 B)
B) (A
(A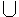 C).
C).
- Absorption. A
 (A
(A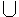 B) is identical to A, and A
B) is identical to A, and A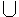 (A
(A B) is also identical to A.
B) is also identical to A.
- Double complementation. - -A is identical to A.
- De Morgan's laws. -(A
 B) is identical to -A
B) is identical to -A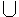 -B. and -(A
-B. and -(A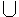 B) is identical to -A
B) is identical to -A -B.
-B.
For complex sets, the rule for determining which elements are in the set may be too complex to state in a single expression. An example is the set of all grammatical sentences in some language, natural or artificial. Such sets are typically specified by a recursive definition:
- First a finite starting set of elements is given.
- Then some operations are specified for generating new elements of the set from old elements.
- Finally, the set is defined to be the smallest set containing the starting elements and all others that can be derived from them by repeated application of the generating operations.
The set resulting from these operations is said to be the closure of the starting set under the given generating operations. As an example of a recursive definition, the set S of all positive integers not divisible by 3 could be specified by intension:
S = {x | x is an integer, x>0, and 3 does not divide x}.But the property x is an integer depends on some prior definition of the set of all integers. The following recursive definition depends only on the operation of adding 3:- Let the set {1, 2} be a subset of S.
- If x is any element of S, then x+3 is also an element of S.
- S is the smallest set that has the above two properties; i.e., S is a proper subset of any other set that has those properties.
All elements of S may be enumerated by starting with {1, 2}. The first stage of adding 3 generates the new elements 4 and 5, adding 3 to them gives 7 and 8, then 10 and 11, and so on. The set S is the closure of the set {1, 2} under the operation of adding 3. A recursive definition is a special kind of definition by intension. Formal grammars define languages by a recursive definition in which the generating operations are specified by a set of production rules.
A set has no duplicate elements. Since all duplicates are discarded in computing the union of two sets, the union operator is idempotent: A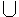 A=A. In some cases, one may want to allow duplicates; therefore, a bag is a collection of things with possible duplicates. Since there may be more than one occurrence of a given element x, the count operator @ is a generalization of the element operator
A=A. In some cases, one may want to allow duplicates; therefore, a bag is a collection of things with possible duplicates. Since there may be more than one occurrence of a given element x, the count operator @ is a generalization of the element operator  . The expression x@A is the number of times the element x occurs in the bag A. Bags are useful for many purposes, such as taking averages: if four men have heights of 178cm, 184cm, 178cm, and 181cm, then the set of those numbers is {178, 181, 184} with the average 181; but the bag of the numbers is {178, 178, 181, 184} with average 180.25.
. The expression x@A is the number of times the element x occurs in the bag A. Bags are useful for many purposes, such as taking averages: if four men have heights of 178cm, 184cm, 178cm, and 181cm, then the set of those numbers is {178, 181, 184} with the average 181; but the bag of the numbers is {178, 178, 181, 184} with average 180.25.
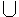 A=A. In some cases, one may want to allow duplicates; therefore, a bag is a collection of things with possible duplicates. Since there may be more than one occurrence of a given element x, the count operator @ is a generalization of the element operator
A=A. In some cases, one may want to allow duplicates; therefore, a bag is a collection of things with possible duplicates. Since there may be more than one occurrence of a given element x, the count operator @ is a generalization of the element operator  . The expression x@A is the number of times the element x occurs in the bag A. Bags are useful for many purposes, such as taking averages: if four men have heights of 178cm, 184cm, 178cm, and 181cm, then the set of those numbers is {178, 181, 184} with the average 181; but the bag of the numbers is {178, 178, 181, 184} with average 180.25.
. The expression x@A is the number of times the element x occurs in the bag A. Bags are useful for many purposes, such as taking averages: if four men have heights of 178cm, 184cm, 178cm, and 181cm, then the set of those numbers is {178, 181, 184} with the average 181; but the bag of the numbers is {178, 178, 181, 184} with average 180.25.A sequence is an ordered bag. To distinguish ordered sequences from unordered sets and bags, the elements of a sequence are enclosed in angle brackets:  178, 184, 178, 181
178, 184, 178, 181 ; the empty sequence is written
; the empty sequence is written 
 . If a sequence has n elements, the elements are numbered from 1 to n (or alternatively from 0 to n-1). A sequence of two elements is sometimes called an ordered pair; a sequence of three elements, a triple; a sequence of four, aquadruple; a sequence of five, a quintuple; and a sequence of n elements, an n-tuple. Historically, the theory of sets was first defined without considering order. On a piece of paper or in computer storage, however, the elements of a set must be listed in some order. Sequences are therefore easier to represent than bags, and bags are easier to represent than sets: a bag is a sequence with the ordering ignored, and a set is a sequence with both order and duplicates ignored.
. If a sequence has n elements, the elements are numbered from 1 to n (or alternatively from 0 to n-1). A sequence of two elements is sometimes called an ordered pair; a sequence of three elements, a triple; a sequence of four, aquadruple; a sequence of five, a quintuple; and a sequence of n elements, an n-tuple. Historically, the theory of sets was first defined without considering order. On a piece of paper or in computer storage, however, the elements of a set must be listed in some order. Sequences are therefore easier to represent than bags, and bags are easier to represent than sets: a bag is a sequence with the ordering ignored, and a set is a sequence with both order and duplicates ignored.
 178, 184, 178, 181
178, 184, 178, 181 ; the empty sequence is written
; the empty sequence is written 
 . If a sequence has n elements, the elements are numbered from 1 to n (or alternatively from 0 to n-1). A sequence of two elements is sometimes called an ordered pair; a sequence of three elements, a triple; a sequence of four, aquadruple; a sequence of five, a quintuple; and a sequence of n elements, an n-tuple. Historically, the theory of sets was first defined without considering order. On a piece of paper or in computer storage, however, the elements of a set must be listed in some order. Sequences are therefore easier to represent than bags, and bags are easier to represent than sets: a bag is a sequence with the ordering ignored, and a set is a sequence with both order and duplicates ignored.
. If a sequence has n elements, the elements are numbered from 1 to n (or alternatively from 0 to n-1). A sequence of two elements is sometimes called an ordered pair; a sequence of three elements, a triple; a sequence of four, aquadruple; a sequence of five, a quintuple; and a sequence of n elements, an n-tuple. Historically, the theory of sets was first defined without considering order. On a piece of paper or in computer storage, however, the elements of a set must be listed in some order. Sequences are therefore easier to represent than bags, and bags are easier to represent than sets: a bag is a sequence with the ordering ignored, and a set is a sequence with both order and duplicates ignored.New sets may be created by combining elements from the universe U in various ways. The cross product of two sets A and B, written A×B, is the set of all possible ordered pairs with the first element of each pair taken from Aand the second element from B. If A is the set {1,2} and B is the set {x,y,z}, then A×B is the set,
{1,x
,
1,y
,
1,z
,
2,x
,
2,y
,
2,z
}.
With the notation for defining a set by a property or rule, it is possible to give a general definition for the cross product A×B:
{x,y
| x
A and y
B}.
The cross product can also be extended to three or more sets. The product A×B×C is defined as
{x,y,z
| x
A, y
B, and z
C}.
Since René Descartes introduced pairs of numbers for identifying points on a plane, the cross product is also called the Cartesian product in his honor.
Inside a computer or the human brain, all sets that are explicitly stored must be finite. But mathematical definitions and proofs are generally simpler if there is no upper limit on the size of sets. Therefore, definitions in computer science often permit infinite sets, but with the understanding that any implementation will only choose a finite subset. Most infinite sets discussed in computer science are assumed to be countable: a countably infinite set is one whose elements can be put in a one-to-one correspondence with the integers. The set of all real numbers is uncountable, but such sets are far beyond anything that can be implemented in computer systems.
The terminology for sets is quite standard, although some authors use the word class for set and others make a distinction between classes and sets. Bags are not used as commonly as sets, and the terminology is less standard. Some authors use the word multiset for a bag. Sequences are sometimes called lists or vectors, but some authors draw distinctions between them. Some authors use the symbol ∅ for the empty set, but the notation {} is more consistent with the notation 
 for the empty sequence.
for the empty sequence.

 for the empty sequence.
for the empty sequence.
Subscribe to:
Comments (Atom)